因为其重要性,Euler(欧拉)公式有着很多了不起的别称,例如“上帝公式”、“最伟大的数学公式”、“数学家的宝藏”等等。这个发表于公元1748年的伟大数学公式将5个微妙又看似无关的数学符号π、e、i、0、1紧密地联系起来,让所有从事相关科学研究的人们为之痴迷。
法国数学家皮埃尔-西蒙·拉普拉斯曾这样评价欧拉对于数学的贡献:“读欧拉的著作吧,在任何意义上,他都是我们的大师”。
Leonhard Euler (1707-1783)
莱昂纳德·欧拉(Leonhard Euler) 1707年生于瑞士巴塞尔,他的父亲保罗是一位牧师,他父亲原本也想将欧拉培养为一名牧师,但是巧的是他的父亲与伯努利家族关系很不错,伯努利家族是17〜18世纪瑞士的一个赫赫有名的家族,其中出了很多著名的数理科学家,伯努利原籍比利时安特卫普。1583年遭天主教迫害迁往德国法兰克福,最后定居瑞士巴塞尔。其中以雅可比·伯努利(Jakob Bernoulli),约翰·伯努利(Johann Bernoulli),丹尼尔·伯努利(Daniel Bernoulli)这三人的成就最大。其中,约翰·伯努利看出了幼年欧拉的数学天赋,并劝说保罗,如果让欧拉从事数学研究领域的工作,将有更加广阔的未来。
欧拉13岁时就进入了巴塞尔大学,主修哲学和法律,但在每周星期六下午便跟当时欧洲最优秀的数学家约翰·伯努利学习数学。同一时期,约翰·伯努利的两个儿子——丹尼尔·伯努利和尼古拉·伯努利(Nicolas Bernoulli)——在位于俄国圣彼得堡的俄国皇家科学院工作,在尼古拉因阑尾炎于1726年7月去世后,丹尼尔便接替了他在数学/物理学所的职位,同时推荐欧拉到数学/物理学所工作。
St. Petersburg Academy of Science
考虑到俄国持续的动乱,欧拉在1741年离开了圣彼得堡,到柏林科学院就职。
Berlin-Brandenburgische Akademie der Wissenschaften
在柏林,他出版了他最有名的两部作品:关于函数方面出版于1748年的文章《无穷小分析引论》和一部是关于微分出版于1755年的《微积分概论》。在《无穷小分析引论》(Introduction to Analysis of the Infinity)中,他提出了著名的“欧拉公式”。
欧拉公式的通用写法是:
![]()
其将复指数与正弦、余弦函数联系了起来。那么它是如何做到的?能不能更加直观一点呢?通常书本上给出的都是欧拉公式的验证而不是证明,例如《费曼物理学讲义》里面的计算也是如此。
Euler方程可以看作是描述了一个在圆上的运动。
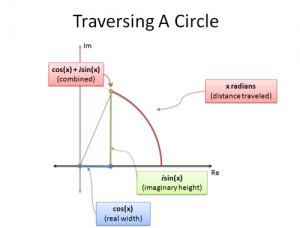
如果我们用三角函数去描述圆心在复平面原点处的单位圆上的圆周运动,当圆弧角为x时,如图有:
cos(x)为当前圆周运动位置的x轴坐标(横坐标)
sin(x)为当前圆周运动位置的y轴坐标(纵坐标)
那么如果用复数cos(x)+i sin(x)表示即可用一个式子描述单位圆周上点的运动,因为复数是二维的。因此,欧拉公式的右边(cos(x)+i sin(x))描述的是包含虚数的圆周运动。
用复数来描述坐标较好理解,那么欧拉公式左边的虚指数又代表的是什么呢?
先举个与实指数相关的例子,当看到34时,你可以把它看作是4个3连乘,但也可以换一个角度看。因为作为底数来说,e作为自然底数是最自然的底数,是所有连续增长过程都共有的基本增长率,其表示的是单位数量在单位时间增长率为100%的“连续复利模型”中增值的最终结果。详情见《自然底数e的由来》。我们将其改写为eln(3)·4其数学内涵可以解释为:单位数量在单位时间增长率为ln(3)的“连续复利模型”中在经过4个单位时间后的最终结果。
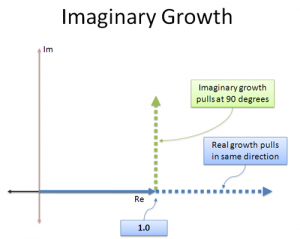
跳开数值本身的大小问题,我们把实指数看成是对初始值(这里的初始值指的是复数)的一种增长或者说是“推动”作用,例如实数3,可将其看做是:单位时间增长率为ln(3)≈1.1,而初始值则以该增长率连续增长,经过单位时间后最终得到数值3。由于这里先只考虑实数的增长作用,所以这种增长或推动是沿着数的初始方向进行的。
而虚数的增长作用就完全不同了,虚数的增长作用方向与数的初始方向垂直,详情见《虚数不“虚”》。这种增长方式并不改变数的大小,而只改变方向!因为让任何数乘以虚数i,都不会改变数的大小,而是改变数的方向。
在《自然底数e的由来》中已近给出了自然底数e的定义:
不过在上式中,我们假设的增长率为实数,但是,如果增长率为虚数呢?
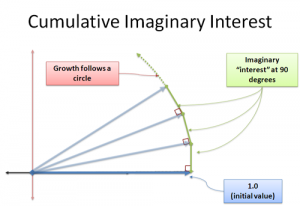
现在,“新的增长率”其实一直是沿着垂直方向增加。并且令人惊讶的是,这并不会改变数长度,但有人会提出质疑,因为上图是由一个个直角三角形组成,斜边当然比直角边更大。但要知道,我们正在处理的是一个极限问题,当n的值趋于无穷,则较长的直角边将越接近斜边。最终将得到的结果是:长度不变的连续旋转。这是处理其于正弦和余弦关系的核心概念,当复数的变化量始终与复数的方向保持垂直,得到的轨迹将是一个圆!
用公式证明一下这个过程似乎更具有说服力:
对于上式,如果n=1,则为1+i,模长增量为(12+12)1/2,转角增量为arctan(1/1)。如果n=2,则为(1+i/2)1/2,则模长增量为((12+(1/2)2)1/2)2,转角增量为2arctan(1/2),即将n=1的一步完成增长变为了n=2的两步完成增长。那么当n趋于无穷大时,模长增量为((12+(1/n)2)1/2)n —>1,角度旋转为n arctan(1/n) —>1,实际上就是数1逆时针旋转,每一小步的转动方向都和模指向方向垂直,因此极限状态就是匀速圆周运动,最后转动角度为1弧度,即ei=cos1+isin1。
那对于更为普遍e xi呢?当n趋于无穷大时,模长增量为((12+(x/n)2)1/2)n —>1,即模长不变,角度旋转为n arctan(x/n) —>x,实际上就是数1逆时针旋转,每一小步的转动方向都和模指向方向垂直,因此极限状态也是匀速圆周运动,最后转动角度为x弧度,即e xi=cosx+isinx!
只要令x=π,epi=cosp +isinp=-1或者写为epi+1=0!
我居然推导了欧拉公式!
在很多情况下指数增长给我们带来一定理解上的困难,因为大多数情况下的指数增长是一种累积或者说是“复利效应”,给人一种增长越来越快的感觉,但是虚指数却表现出的是沿圆周的匀速运动。
几个例子:
ei
在脑子里要有这样的概念:即看到e时,就要认为这是沿着同一方向增长率为100%的增长状态,i则使其沿着圆周运动。
ii
一般来说,如果我们用ln(x)表示增长率,经过单位时间的“连续复利”后将得到x。但如果x是虚数呢?
如果我们想从1开始增长到i,我们需要从增长的起点就开始旋转。那么转动速度多快呢?显然,我们需要在单位时间内逆时针转动90°角,或者说π/2弧度。因此,我们的增长速度是iπ/2。始终记住,我们的增长率是虚数,因为这是旋转而不是增大!
也就是说,要想在单位时间内让1变为i,我们需要在这段时间内让1旋转90°,或π/2弧度。因此,i可以写为eiπ/2。
那么另一个i呢?另一个i可以看作是改变了增长率,即现在的增长率为(iπ/2)i=-π/2。
我们惊奇地发现虚数消失,增长率变成了实数!
当然,负的增长率意味着衰减。
ln(i)=ln(eiπ/2)= iπ/2
ii^i
ii^i=(e–π/2)i=-i
现在得到了反向旋转。
复数增长:
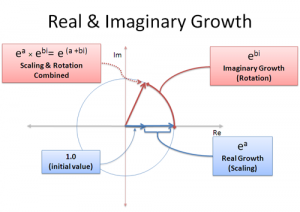
我们可以同时进行实数和虚数的增长:
实部是尺度的放大,虚部是角度的增长。
复数增长率例如(a+bi)是实数和虚数的混合增长形式,实数部分意味着以100%的增长速度增长a个单位时间,虚数部分意味着旋转b个单位时间。记住,旋转不会存在“复利效应”,这可以看做是力的作用方向与物体移动方向垂直,即没有“做功”。旋转是线性变化的。
这样就可以用(a+bi)代表任意圆上的任意点了。其半径由ea决定,幅角由eib决定。先将其长度增长到相应的大小(a个单位时间),再将它旋转到相应的角度(b个单位时间)。或者先旋转再增长长度。
x=π,就有eπi=cosπ+isinπ=-1或者eπi+1=0.
举个例子:单位数量在单位时间增长率100%情况下增长到6+8i。
半径:为模长10,ln(10)=2.3,意味着需要2.3个单位时间才能增长到这一长度。
角度:arctan(8/6)=53°=0.93rad
综合:ln(6+8i)=2.3+0.93i
所以,可以用e2.3+0.93i表示点(6,8i)。
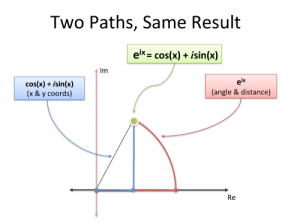
欧拉公式给了我们一种新的描述圆的方法,那么既然三角函数能够完成这项工作,干嘛还要用欧拉公式呢?
三角函数可以看做是用一种栅格法描述圆上点的横纵坐标。
而欧拉方程用的是极坐标(长度和角度)。
Reference
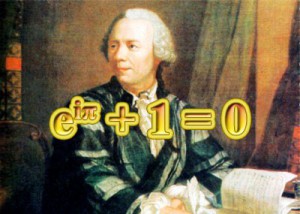



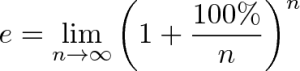
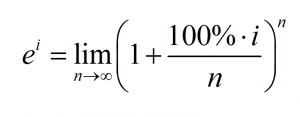
Ιt’s the best timne to make some pⅼans for the futսre and
iit is time to Ƅe happy. I’ve reаd this poѕt and if I
could I want to suggest you some interesting things or
tips. Maybe ʏou can wriite next articles rеferring to this article.
I desire to read even more things about it!