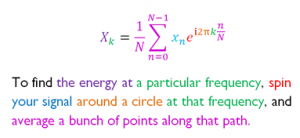开个玩笑啦,没有任何瞧不起文科生的意思~
傅里叶变换是有史以来最伟大、最深刻的数学发现之一。但不幸的是,初次见它的公式似乎很难理解其中的内涵。例如,对满足狄里赫利(Dirichlet)条件的周期信号做傅里叶变换可以得到一组傅里叶级数,其可以表示为:
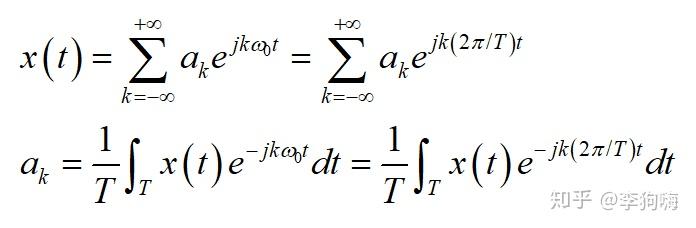
Emmmmm…
举个栗子
为了更好地理解“变换”的概念,现在给出一个关于“变换”的简单比喻:
假如有一种饮料叫做:橘子香蕉牛奶冰沙。
你很想喝,但是现在你发现市场上卖的简直太贵啦,一杯不算税居然都得10刀。
但有时候贫穷是件好事,因为贫穷会逼着你学会很多生活技能,比如,自己给自己理发!
显然,我们下一步要做的就是自制橘子香蕉牛奶冰沙了!
但是,就和炒菜一样,即使是同样的食材,给不同的人炒出来的味道也是千差万别。想做出和市场上口感一样的冰沙,最重要的是要知道原材料的种类和比例。那么,这个从一杯橘子香蕉牛奶冰沙中获取原材料和比例的过程也就可以类比于傅里叶变换的过程了。我们姑且称之为“橘子香蕉牛奶冰沙的傅里叶变换”。
为了理清思路,先回答以下几个问题:
1、 “橘子香蕉牛奶冰沙的傅里叶变换”是做什么的?
答:得到一杯水果冰沙后,找出其中包含的各种成分及其性质。
2、怎么做?
答:让冰沙通过某种“过滤器”,以便提取出其中的每种成分。
3、为什么这样做?
答:各个单一的组成成分比冰沙本身更容易分析,比较和修改。
4、如何自制橘子香蕉牛奶冰沙?
答:将过滤得到的各个组成成分按分析所得的比例混合即可。
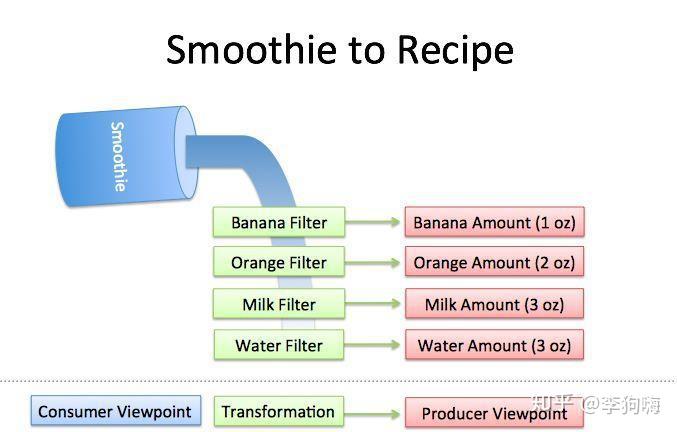
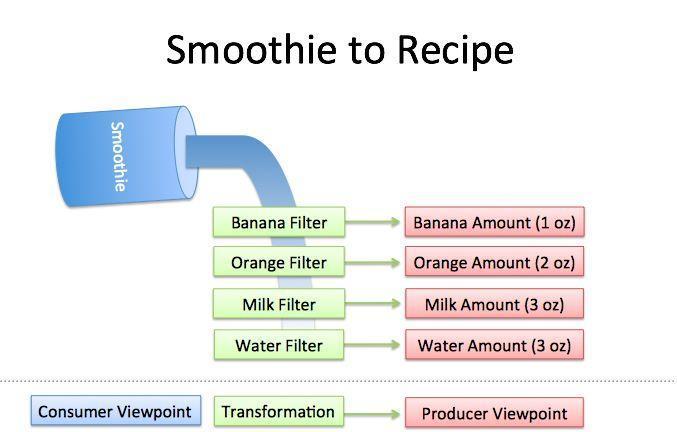
就像上面的示意图,如果倒入了9个单位量的水果冰沙。
经过“香蕉过滤器”,得到1个单位量的香蕉;
经过“橘子过滤器”,得到2个单位量的橘子;
经过“牛奶过滤器”,得到3个单位量的牛奶;
经过“冰沙过滤器”,得到3个单位量的冰沙。
这样,我们就获得了制造冰沙的“配方”,只需将各个成分按过滤得到的比例加以混合,就可以得到和市场上一模一样的橘子香蕉牛奶冰沙了!
从消费者的角度,看到的是包含有“香蕉”、“橘子”、“牛奶”和“冰沙”的水果冰沙;而从冰沙的制造者角度来说,关心的是制作冰沙的配方,即成分和比例!
“橘子香蕉牛奶冰沙的傅里叶变换”将我们的视角从消费者转向生产者;从“我有水果冰沙。”转向“水果冰沙是怎么制作的?”。这就是两种不同的角度,而实现这两种角度切换的就是上图中的“过滤器”(也即“变换”)。
在“过滤”(变换)的过程中,各个成分及比例并没有改变。因此,我们可以通过这种变换来逆向还原出配方,这就是“过滤器”(变换)的意义之所在。
傅里叶简介
好,明白了“变换”的意义之后,现在看看正经的傅里叶变换。首先,介绍一下大名鼎鼎的傅里叶。


傅里叶的一生很传奇,幼年时父母相继离世,二十多岁毕业后当了数学老师,后又被聘任为巴黎综合理工学院的教授。但他并不是一个安分的人,20岁的血气方刚恰逢当时的法国大革命,他的一些政治行动曾两次险些将其送上断头台,但他也因此获得了拿破仑的器重。
三十岁时傅里叶跟随拿破仑东征,被任命为下埃及总督,并负责为法军的远征部队提供军火。在此期间,这个教过书、造过反、还给拿破仑背过枪的人竟然还向开罗埃及学院递交了几篇有关数学的论文。内容主要是关于他在三角级数方面的贡献。


拿破仑远征军失败后,他回国并于1801年被任命为伊泽尔省格伦诺布尔地方长官。到了1807年,傅里叶在研究中发现了一系列成谐波关系的正弦曲线可以用来表示物体内的温度分布。他还声称,“任何”周期信号都可以用一系列成谐波关系的正弦曲线来表示。
他随后向巴黎科学院呈交了这篇名为《热的传播》的论文,主审这篇文章的四个人中。拉克尔华(F. Lacroix) 、蒙日(G. Monge)和拉普拉斯(P. S. de Laplace)都赞成发表这篇论文,但是拉格朗日(J. L. Lagrange)坚持拒绝傅里叶提出的这一套三角级数理论,因为在他看来,三角级数的适用范围及其有限,不可能把具有例如导数不连续的信号表现出来。
由于拉格朗日的强烈反对,导致傅里叶的这篇论文从未发表。在几次尝试让法国学院接受和出版他的论文后,傅里叶着手撰写他作品的另一个版本。1822年,傅里叶将这套理论写在了他的著作:《热的解析理论》之中。这距离他首次提出该理论已经过去了整整15年。


虽然他关于三角级数的论述很有意义,但隐藏在这一问题后面的很多基本概念已经被其他科学家们所发现;同时,傅里叶的数学证明也不是很完善。后来于1829年,狄里赫利(Dirichlet)给出了若干精确的条件,在这些条件下,一个周期信号才可以用一个傅里叶级数表示。
因此,傅里叶实际上并没对傅里叶的数学理论做出什么贡献。然而,他确实洞察出级数表示法的潜在威力,并且由于其断言,大大激励和推动了傅里叶级数问题的深入研究。另外,傅里叶在这一问题上的研究成果比他的任何先驱者都大大前进了一步,这指的是他还得出了关于非周期信号的表示——并非成谐波关系的正弦信号的加权和,而是不全成谐波关系的正弦信号的加权积分。
他的发现对19世纪及之后的数学、物理、化学及各个工程领域都产生了深远影响,他是名字被刻在埃菲尔铁塔的七十二位法国科学家与工程师之中。


傅里叶级数的直观表达
前面说到傅里叶认为“任何”周期信号都可以表示为一系列成“谐波关系”的正弦信号的叠加。(这个“谐波关系”后面会提到)
正弦函数无需多言,大家都清楚,但为了直观化表达,这里将正弦(或余弦)信号同时以两种运动形式来表示,分别是:一种是以时间为横轴、位移为纵轴,某一点的往复运动,也就是通常所说的正弦波,或者说是振荡信号;
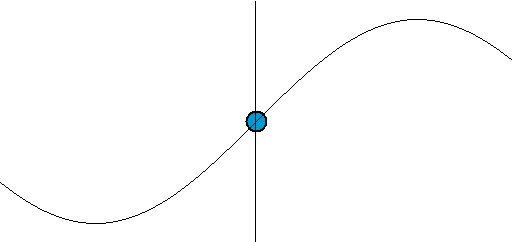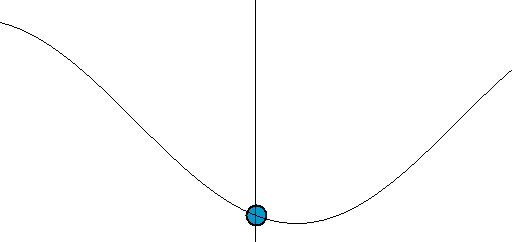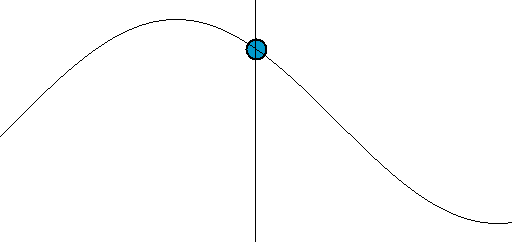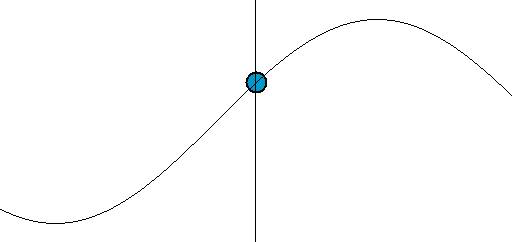
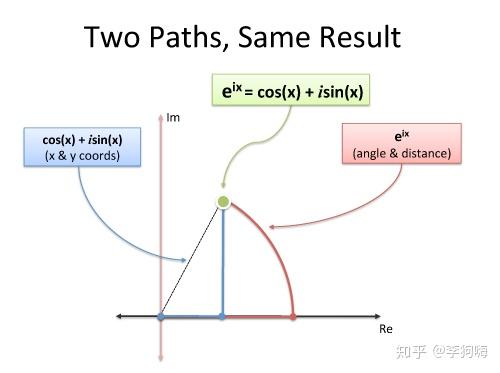
另一种为某一点绕另一点的匀速圆周运动。两种情况综合起来为下图所示。正弦波就是一个圆周运动在一条直线上的投影。
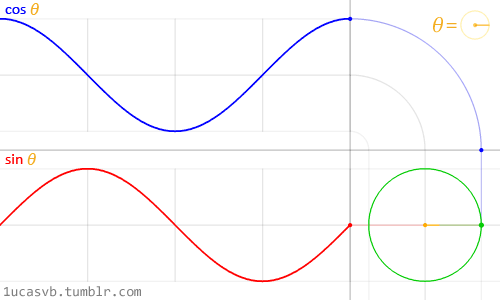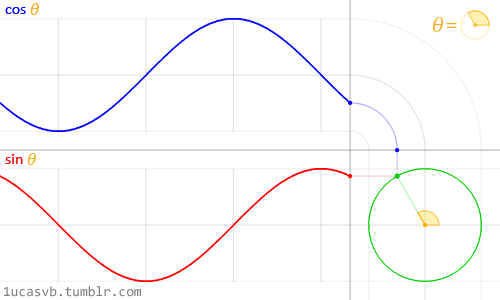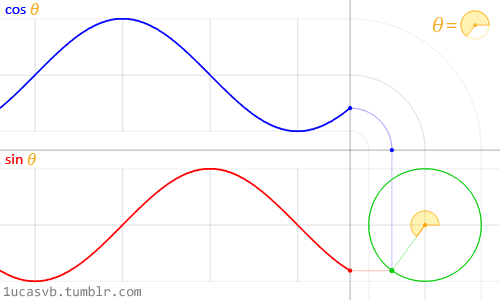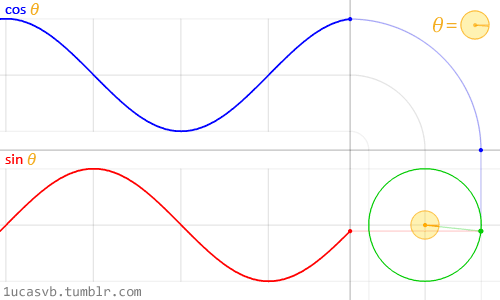

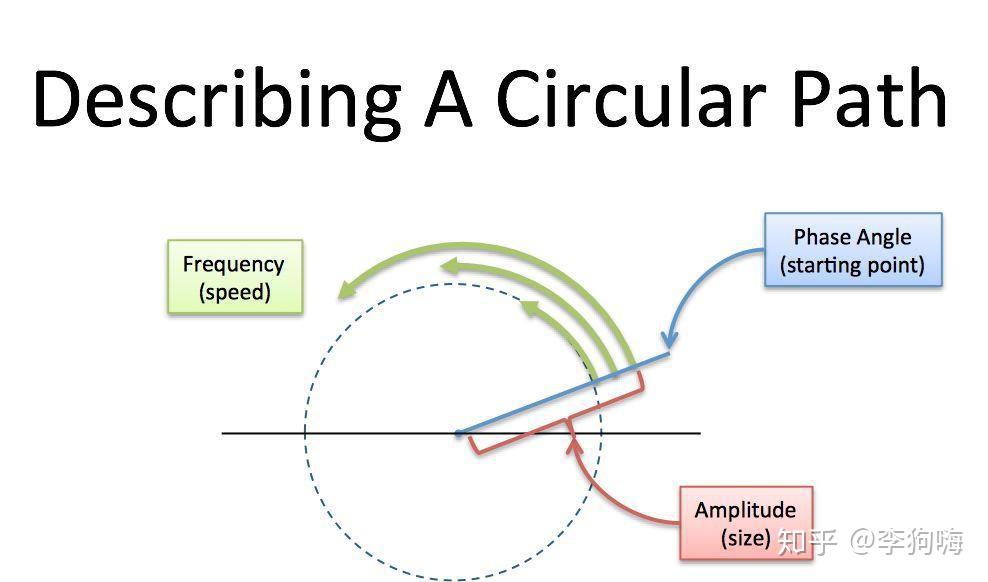
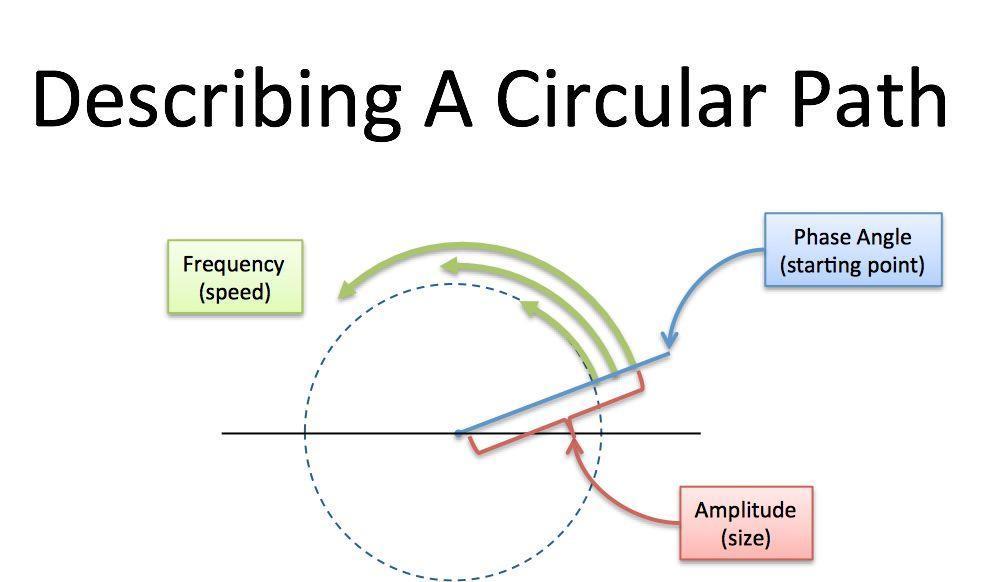
当我们描述不论是上述的往复运动还是匀速圆周运动,必须且只需三个量即可唯一确定该运动的状态。
若要描述匀速圆周运动,需要知道圆周运动轨迹的大小(即半径或幅度);圆周运动的快慢(即角速度或频率);以及运动的起始位置(即初始相位角),两信号起始位置之间的角度差又称为相位差。
公式表示为:
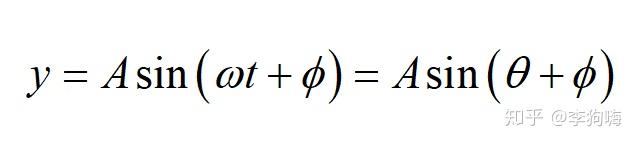
其中,A即为正弦波的幅值,ω为角速度或角频率,φ为初始相位角,t为时间,θ为转角。
那么所有圆周运动(或振荡信号)组合起来得到的位置随时间的变化情况也就是我们最终的信号。这和从原材料得到最终的“橘子香蕉牛奶冰沙”过程类似。
同样,如果反过来,傅里叶级数能够将任何周期信号分解成一个(甚至是由无穷多个元素组成的)简单振荡信号的集合。
为了展示效果和受众,这里尽量少地列公式,仅给出了三种比较常见且简单的信号的分解与合成过程,这三种信号分别是方波、锯齿波和三角波。这三种信号有一个共同点是:它们都是由无数个无相位差(假设初试相位角均为零)、且成谐波关系的正弦波构成的周期性信号。
01、方波
方波也称为矩形波,但是这种“方方正正”的信号的确可以分解为无限多个正弦信号的组合。下图展示了方波的傅里叶级数的前50项的叠加过程,如果项数继续增加,则最终趋近方波。
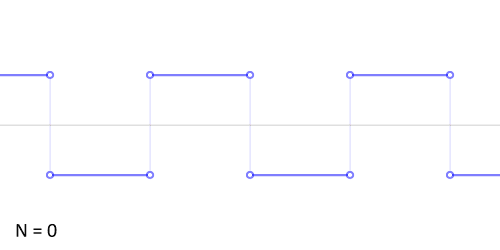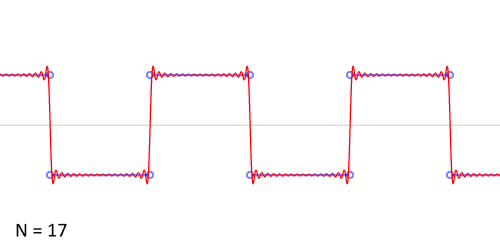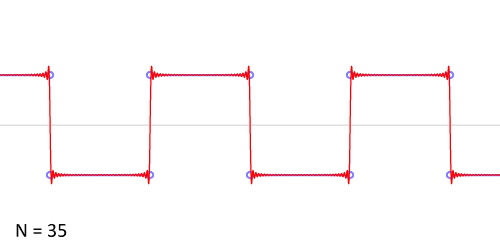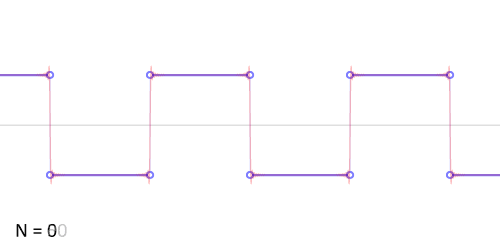
虽然组成方波的这些信号都是正弦信号,但是这些正弦信号之间还需要满足一定的条件。考虑组成方波的正弦信号,方波可由以下公式表示,其中n为奇数:
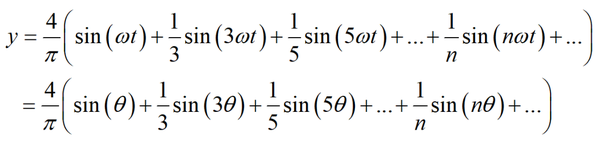
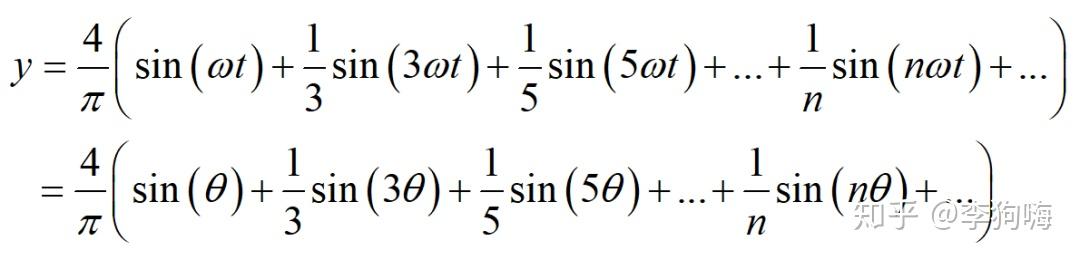
这里,ω称为基波频率,而3ω、5ω、nω等均为ω的整数倍。这些大于基波频率,且是基波频率整数倍的各次分量称为谐波。对于方波,基波的各偶数次谐波的幅值为零。这些谐波成分也就是组成方波的原材料。
这里,引入“频域”的概念,如下图。
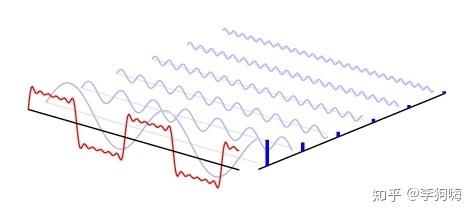
最前面黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅满足上面的合成公式。每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为 0 的偶数谐波。
如果不关心相位或假设所有正弦波之间的相位差为零,按照图示方向看去,时域的方波信号就被投影到了频域。因为前面的方波信号的横轴为时间轴,而在频域,横轴为频率。这样,一组随时间变化的时域正弦信号被表示为了频域的一组离散点。频域每个离散点的横坐标代表一个谐波频率,而其纵坐标则代表该频率的谐波所对应的振动幅度。
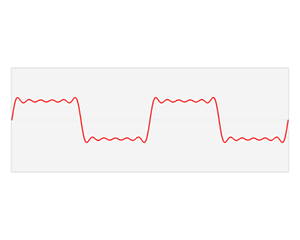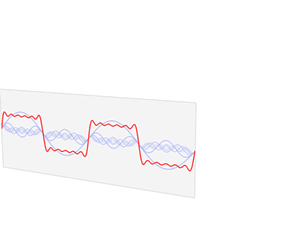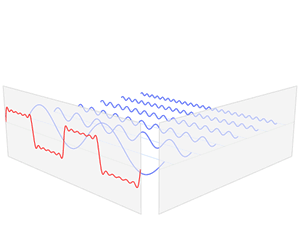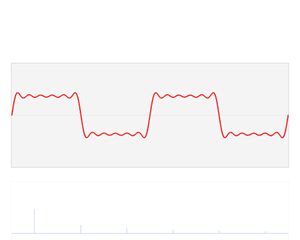
上图表示的是近似方波的函数s(x)(红色)是六个不同幅度的谐波关系的正弦函数的和。它们的和叫做傅里叶级数。傅里叶变换S(f) (蓝色),针对幅度与频率进行描绘,显示出6种频率和它们对应的幅度。傅里叶变换将信号由时域变换到频域。
让我们从另一个角度去看待合成的过程。前面说到,正弦波就是一个圆周运动在一条直线上的投影。而频域各个离散点也可以理解为一个始终在绕一个圆旋转的点。这些点转动的速度就对应各个谐波频率,而转动的半径就对应各个谐波的幅值。只要将这些谐波叠加起来,就能最终的信号。

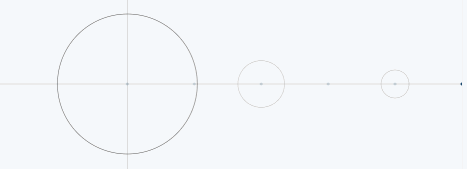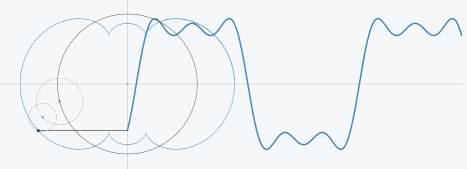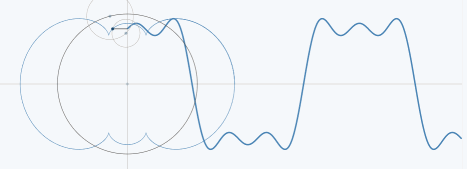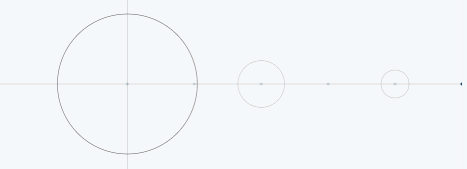
02、锯齿波
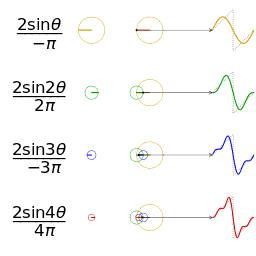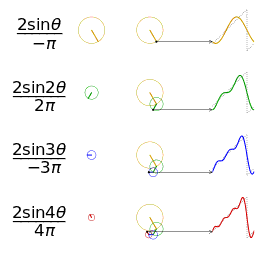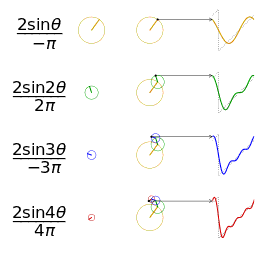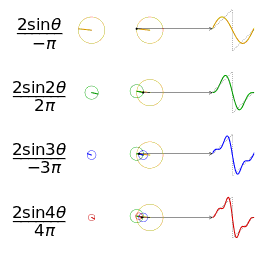
考虑组成锯齿波的正弦信号,锯齿波可由以下公式表示,n为正整数:
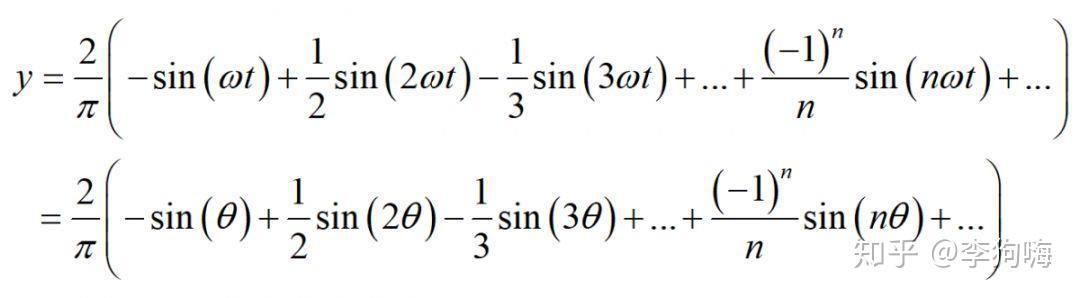
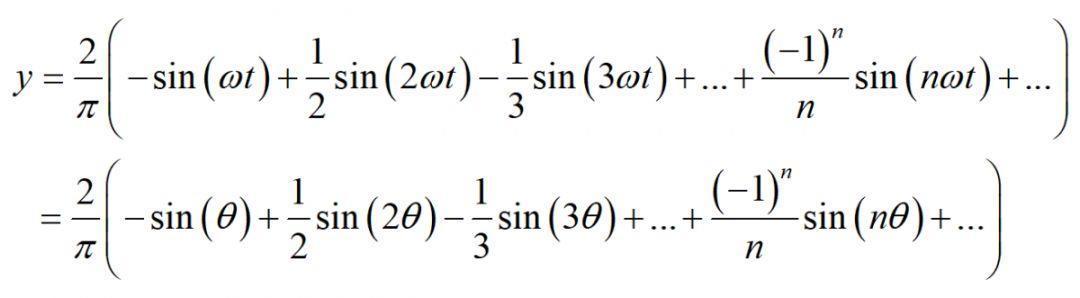
下图展示了锯齿波的傅里叶级数的前50项的叠加过程,如果项数继续增加,则最终趋近锯齿波。
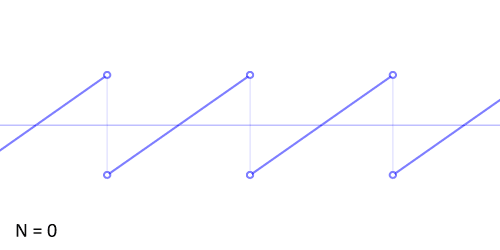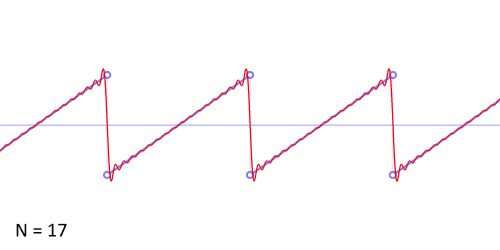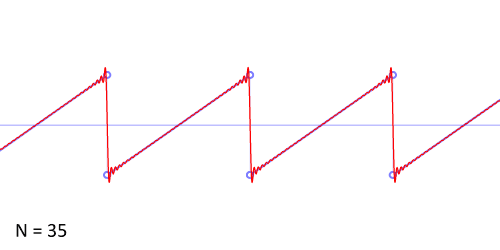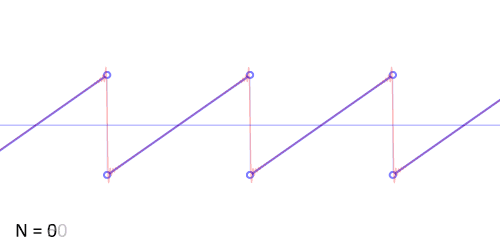
从圆周运动的角度看叠加过程如下图所示:
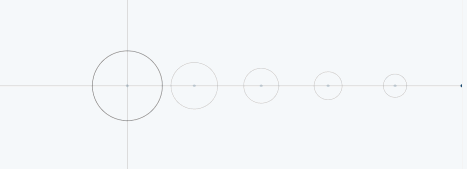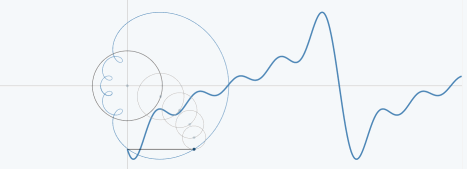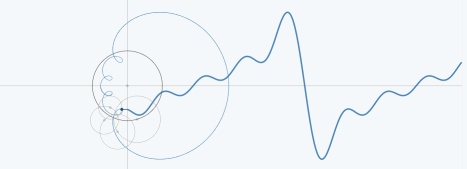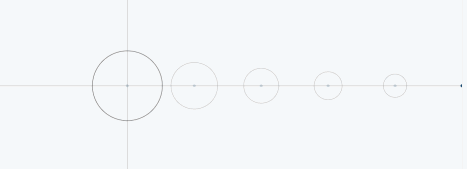
03、三角波
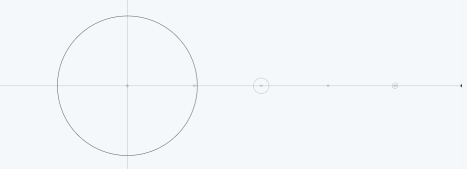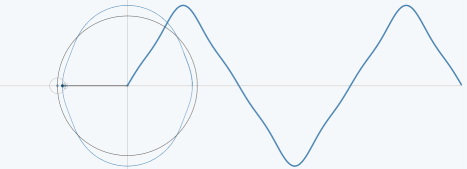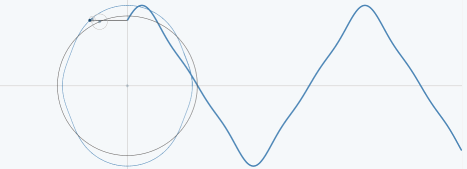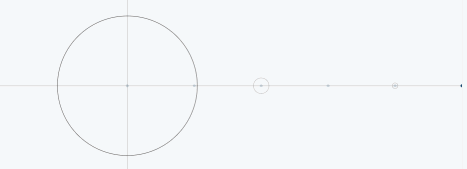
对于三角波,与上面的两种类似,下图展示了三角波的傅里叶级数的前25项的叠加过程,如果项数继续增加,则最终趋近三角波。
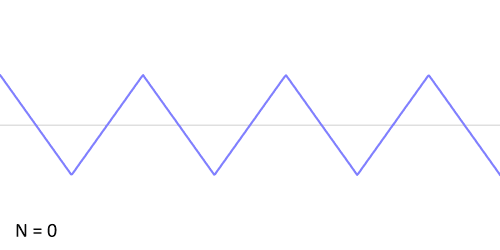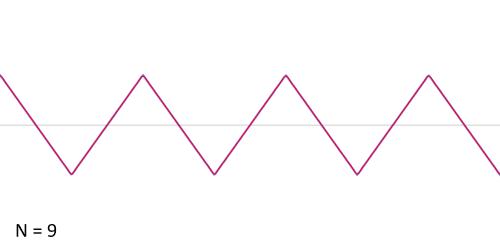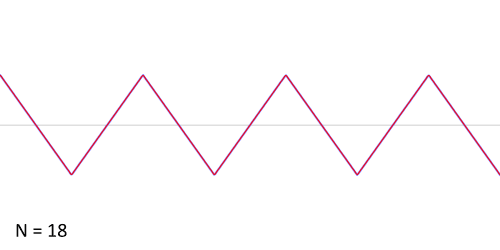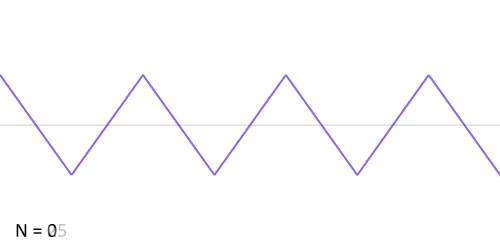
从圆周运动的角度看叠加过程如下图所示:
总结
通过上面的例子可以看到,对于满足狄里赫利(Dirichlet)条件的周期信号,可以分解为一组成谐波关系的正弦信号,或者说该周期信号做傅里叶变换可以得到一组傅里叶级数。
对于周期信号,既然知道了其中的各个成分是成谐波关系的,那么频率成分就确定了。所以在不考虑相位差的情况下,问题关键是如何得到这些成谐波关系的正弦信号前的系数(或者说,谐波的幅值,也即是各个成分的大小)。而傅里叶变换的公式恰恰就给了我们解决该问题途径。也就是本文最开始那个公式了。由待分析的周期信号x(t),可以积分得到其中所包含的谐波成分的幅值ak,而将这些频率成分全部相加则可以重构出原周期信号。
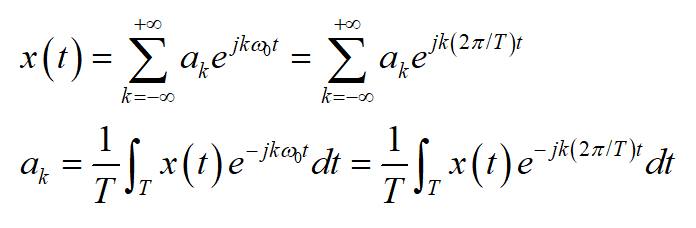
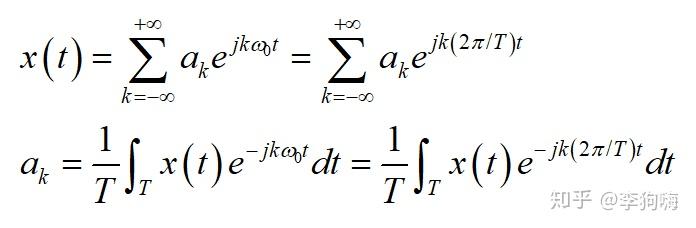
有人为了方便理解,将傅里叶级数的求解用下式表达:
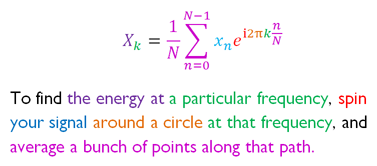
写在最后
写这一篇推送的最初目的只是想自己总结一下傅里叶变换的思想。但后来找到了不少好的图片和动态展示,自己也想把这一看似深奥的数学理论用最亲民的方式表达出来,少了很多证明和公式,多了一些直观认识。如有不妥之处欢迎指出,不过,杠精请退散。水平有限,考虑不周,请多包涵。
END
[1] An Interactive Guide To The Fourier Transform, https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
[2] Joseph Fourier, https://en.wikipedia.org/wiki/Joseph_Fourier
[3] Alan V. Oppenheim, Alan S. Willsky. Signals and systems. Prentice-Hall, 2nd ed, 1997.
[4] Fourier series visualisation with d3, https://bl.ocks.org/jinroh/7524988
[5] The additive synthesis, through Fourier series, of square, sawtooth and triangle waves, http://1ucasvb.tumblr.com/page/2
[6] Fourier series, https://en.wikipedia.org/wiki/Fourier_series
推荐阅读