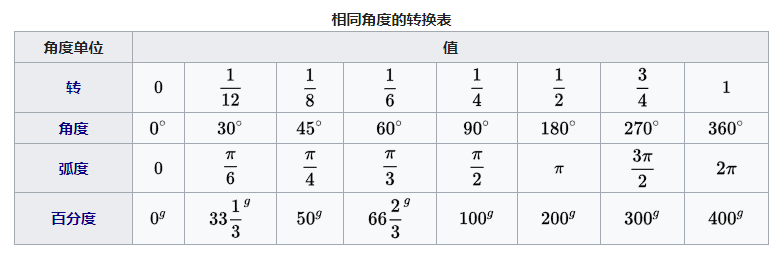
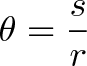一圈是360°，这听起来似乎很自然，自然到不会去问为什么。我们习惯于用360°形容转一圈的角度，但当学习进一步深入，就开始接触一个新的用于描述角度的单位——弧度。而科学家说：“弧度让数学更简单！”那这是为什么呢？

首先说说为什么一圈是360°。

我们将地球绕太阳一周定义为理论上的一年。其实际所需的时间约为365.25天，人们为了取整方便，就定义了闰年，每隔4年出现一次，在365天的基础上加一天，正好也能够补偿前3年所累计的误差。

那有人就会问了，既然如此，为什么一圈是360°，而不是365°或是365.25°？

因为360°容易被整除，360的真因数除了1和自身以外，一共有22个（2、3、4、5、6、8、9、10、12、15、18、20、24、30、36、40、45、60、72、90、120、180），所以很多特殊角的角度都是整数。另外，这也更加符合以60为进制的“巴比伦数字”系统。

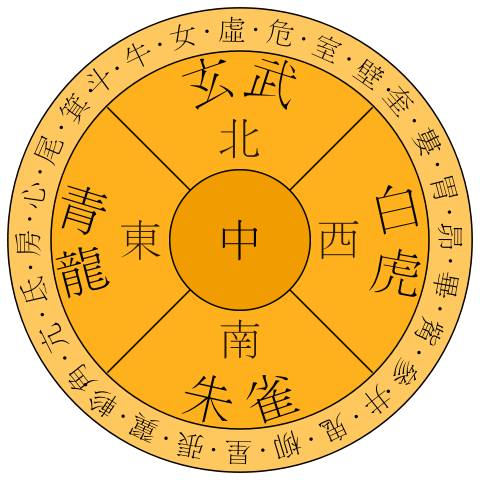
如果说这还不具有说服力，还有一个例子，就是中国的二十八星宿(xiu，读第四音)。（看到这张图，突然想到了“物华天宝，龙光射牛斗之墟；人杰地灵，徐孺下陈蕃之榻”。）

（图片来源：Wikipedia）

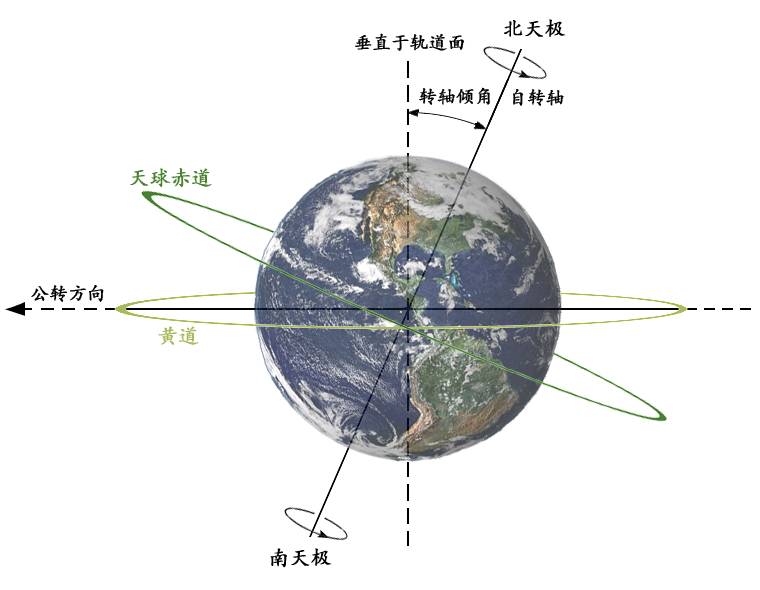
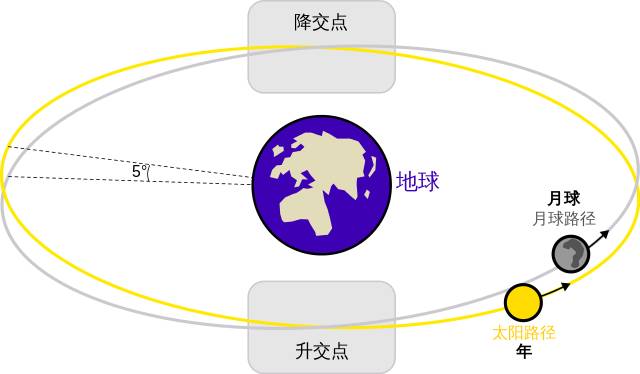
由于月球绕行地球一周为27.3日，所行路径为白道（与黄道夹角5.145度），古人将白道圈分成28段，即将黄道和天赤道附近的天区划分为二十八个区域，因此月球大约每日可入宿到28段中的一个星宿内。二十八宿又分为四组，每组七宿，与东西南北四个方位和青龙、白虎、朱雀、玄武四种动物形象相配，称为四象。

（图片来源：Wikipedia）

（图片来源：Wikipedia）

而因为潮汐锁定而形成月球的同步自转（自转周期和公转周期相等），导致月球永远只能一面面对地球（当然这一特点和星宿划分并没有什么直接关系）。

（图片来源：Wikipedia）

总之，星宿就是以行星、恒星运动周期来划分圆周的一个典型例子。

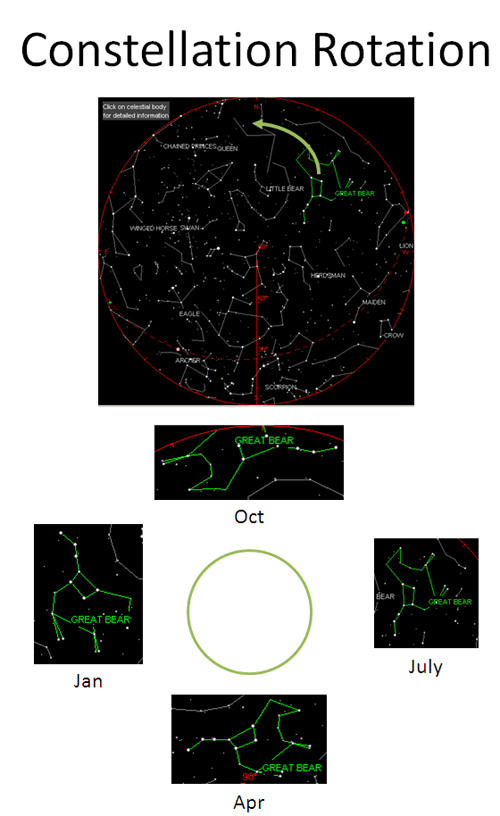
中国人看星宿，西方人看星座。下图是2008年一年间纽约夜空所观察到的大熊座（Great Bear，中国称为北斗七星）的位置变化情况。可以看出，每过一年就会循环一圈。

（图片来源：Betterexplained）

以绕太阳一周为周期似乎是一个不错的方法，对于生活在地球上的人类来说，这很自然。但如果参考标准变化，就会发现这样的划分其实掺杂了太多的人为因素。

例如，如果人类生活在火星，而不是地球上，或许人们就会把一个圆周定为680°，因为一个火星年大约是680天。而对于某些建筑或土木工程人员，他们可能更习惯用梯度，即将一个圆周划分为400份。

（图片来源：Wikipedia）

为了避免这种任意性所带来的标准不统一，人们需要一个新的定义来定义角度。因此有了“弧度”的概念。

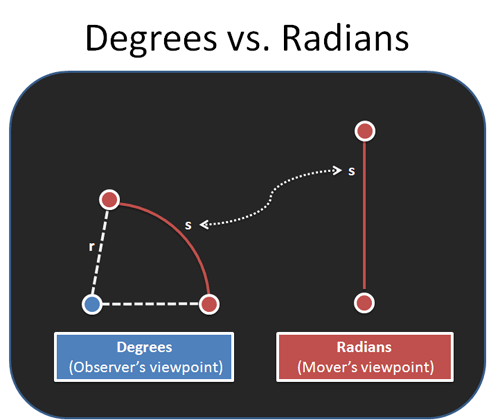
可以把“度数”的定义视为是一种以自己为中心来看待角度问题的方法，而将“弧度”的定义视为是一种站在他人立场上看待角度问题的方法。听起来有些绕口。

举个例子，你站在操场中心，另一个人与你之间有一定的距离且绕着你沿圆周跑步，你要做的就是保持你的脸始终朝向那个人。假设那个人跑的长度为S，根据你和那个人之间的距离r 就可以计算出你的头偏转的角度。

（图片来源：Betterexplained）

也就是说“度数”关心的是你的头偏转的角度，而“弧度”则关心的是那个人奔跑的距离。其本质区别在于参考对象变了。

弧度的定义就是：以某一点为中心（圆心点，对应于上图中的蓝色圆圈），运动点（对应于上图中的红色圆圈）绕圆心点做圆周运动的长度除以运动点到圆心点的距离。

通常写为下式：

因此，一圈是360°或2π弧度，1弧度约为360/(2π)≈57.3°。

那么，弧度为什么会给工程带来方便呢？其原因就在于弧度是站在“运动点”的角度看问题，而不是站在“圆心点”的角度看问题。

例如，在测量某些转速时，人们通常使用的是rpm(Revolutions per minute)，即每分钟多少转，而不是每秒钟或每分钟多少度。

举一个更具体的例子，就能感受到弧度到底方便之处。假设你有一辆汽车，汽车轮胎半径2米（夸张一下），先用角度的概念提问，若车轮每秒转2000°，问汽车前进的速度有多快？

计算方法是：

1、计算每秒轮胎转过的圈数：2000/360=50/9 圈；

2、计算每秒转过的周长：2×π×2×50/9=(200π/9) m/s。

现在用弧度的概念提问，若车轮每秒转6弧度，问汽车前进的速度有多快？

计算方法是：

直接用轮胎半径乘以每秒转动的弧度：2×6=12 m/s。

嗯嗯，这样方便多了。果然老司机。

Reference

[1] Intuitive Guide to Angles, Degrees and Radians; https://betterexplained.com/articles/intuitive-guide-to-angles-degrees-and-radians/

[2] Degree(angle); https://en.wikipedia.org/wiki/Degree_(angle)

[3] Babylonian numberals; https://en.wikipedia.org/wiki/Babylonian_numerals

[4] Lunar node; https://en.wikipedia.org/wiki/Lunar_node

[5] Tidal locking; https://en.wikipedia.org/wiki/Tidal_locking